Моделирования движения. Задания для самостоятельной работы

| Моделирование в электронных таблицах

Уроки 17 - 18
Моделирование в электронных таблицах

Моделирование движения тела под действием силы тяжести

Примеры движения под действием силы тяжести хорошо известны. Это и падение тела с некоторой высоты, и движение тела, брошенного вверх с некоторой скоростью, и движение тела, брошенного под углом к горизонту. Если в таких задачах не учитывать силу сопротивления воздуха, то все перечисленные виды движения описываются известными формулами. Но задачи, в которых сопротивление воздуха учитывается, не менее интересны.

ЗАДАЧА 3.24. Поражение цели

I этап. Постановка задачи

ОПИСАНИЕ ЗАДАЧИ

Мальчики играют в бадминтон. Порыв ветра подхватил волан и отнес его на ветви дерева. Предстоит нелегкая задача - достать волан. Задачу можно решить несколькими способами. Каждый из способов имеет свои плюсы и минусы.

Можно, например, залезть на дерево. Но это очень опасное занятие: ветки дерева чем выше, тем тоньше. Велика вероятность падения. Можно спилить дерево. Но, видимо, еще никто не опробовал такой путь решения задачи. Если бы все выбирали такой способ решения задачи, то давно бы уже не осталось ни одного дерева. Можно ждать, когда волан упадет сам, подхваченный очередным порывом ветра. Наиболее часто волан пытаются сбить камнем. Выберем эту модель поведения и мы. Тем более, что нам известны законы движения тела.

ЦЕЛЬ МОДЕЛИРОВАНИЯ

Исследовать движение тела, брошенного под углом к горизонту. Подобрать начальные значения скорости и угла бросания так, чтобы брошенное тело попало в цель.

ФОРМАЛИЗАЦИЯ ЗАДАЧИ

Примечание. Чтобы задать точность попадания △ , надо учитывать размеры тела.

Точность попадания △ должна быть не более половины наименьшего геометрического размера тела.

Так, например, если цель - волан размером в диаметре примерно 7 см, то △ = 3,5 см. Если цель - баскетбольное кольцо диаметром 40 см, то △ = 20 см. Если цель - аэростат высотой 5 м, то △ = 2,5 м.

II этап. Разработка модели

ИНФОРМАЦИОННАЯ МОДЕЛЬ

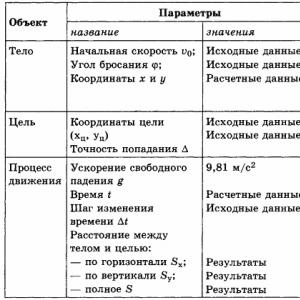
Характеристики объектов и процесса представим в виде таблицы.

Параметры движения тела представлены на рисунке 3.4. Движение тела, брошенного под углом к горизонту, описывается формулами

КОМПЬЮТЕРНАЯ МОДЕЛЬ

Для моделирования выберем среду табличного процессора. В этой среде табличная информационная и математическая модели объединяются в таблицу, которая содержит три области:

♦ исходные данные;
♦ промежуточные расчеты;
♦ результаты.

1. Заполните область исходных данных по образцу.

Столбцы А, В, С, D, Е, F заполнить сверху вниз аналогичными формулами.

2. Заполните область промежуточных рассчетов и результатов.

ПЛАН ЭКСПЕРИМЕНТА

ТЕСТИРОВАНИЕ

ЭКСПЕРИМЕНТ 1

Исследовать движение тела.

ЭКСПЕРИМЕНТ 2

Исследовать изменение движения тела при изменении начальной скорости.

ЭКСПЕРИМЕНТ 3

Исследовать изменение движения тела при изменении угла бросания.

ЭКСПЕРИМЕНТ 4

Изменяя начальную скорость и угол бросания, исследовать характер движения тела и его положение по отношению к цели.

ЭКСПЕРИМЕНТ 5

Изменяя исходную начальную скорость и угол, подобрать значения так, чтобы брошенное тело попало в цель с заданной точностью.

ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ

ТЕСТИРОВАНИЕ

1. Заполните столько строк расчетной таблицы, пока координата у не станет меньше нуля.

2. Сравните результаты тестового расчета с результатами, приведенными в примере расчета. Ниже в таблице представлено несколько строк с результатами расчетов по приведенным исходным данным.

3. По столбцам В и С построить диаграмму движения. Пример представлен на рисунке 3.6. Для построения диаграммы возьмите столько расчетных значений, чтобы кривая пересекла горизонтальную ось х .

4. Как определить, сколько расчетных точек надо взять для построения диаграммы?

Вывод. Для построения диаграммы надо взять расчетные значения, у которых координата y больше 0, и одно отрицательное значение.

ЭКСПЕРИМЕНТ 1. Исследование движения тела

1. По диаграмме тестового примера опишите, как движется тело.

2. Объясните, как по диаграмме определить точку наивысшего подъема тела.

3. Объясните, что на диаграмме обозначает точка пересечения кривой с горизонтальной осью х. Как по таблице расчетов определить эту точку?

4. Определите по диаграмме, на каком расстоянии от точки броска тело упадет на землю.

5. Определите по таблице расчетов:

Наибольшую высоту подъема;
время движения до наивысшей точки;
расстояние от точки броска до точки падения на землю;
время движения до падения.

В свободной области электронной таблицы запишите результаты исследования движения тела по предложенному образцу.

6. Введите другой вариант исходных данных, заполните для них таблицу результатов эксперимента.

ЭКСПЕРИМЕНТ 2. Зависимость движения тела от начальной скорости (угол бросания неизменный)

1. Изменяя начальную скорость от 5 до 20 м/с, проследите, как изменяется наибольшая высота подъема (координата у)

2. Проследите, как изменяется дальность полета (координата x) при увеличении начальной скорости.

3. Проведите расчеты для некоторого угла и результаты исследований сведите в таблицу (таблица 2), составленную на свободном поле электронной таблицы.

4. Запишите в таблицу выводы по результатам эксперимента: как изменяется высота и дальность полета при изменении начальной скорости (при неизменном угле бросания)?

ЭКСПЕРИМЕНТ 3. Зависимость движения тела от угла бросания (начальная скорость движения неизменна)

1. Проведите расчеты по модели, увеличивая угол бросания от 5° до 85° и оставляя неизменной начальную скорость (например, 15 м/с).

2. Проследите изменение высоты подъема (координата у) при увеличении угла бросания, начальная скорость неизменна.

3. Проследите изменение дальности полета (координата x) при увеличении угла бросания.

4. Результаты расчетов сведите в таблицу на свободном поле электронной таблицы (таблица 3). 

5. Запишите в таблицу выводы по результатам эксперимента: как изменяется высота и дальность полета при изменении угла бросания (при неизменной начальной скорости)?

ЭКСПЕРИМЕНТ 4. Исследование характера движения тела и его положения по отношению к цели

На рисунке 3.7 показаны варианты расположения кривой движения тела по отношению к цели. Их можно охарактеризовать следующим образом:

1. Тело при движении не достигает высоты, на которой расположена цель, и падает на землю, не достигая X ц .

2. Тело при движении не достигает высоты, на которой расположена цель, но падает на землю дальше X ц .

3. Тело при движении поднимается выше Y ц , но падает на землю, не достигая X ц .

4. Тело при движении поднимается выше Y ц и падает на землю дальше X ц .

В столбцах D, Е и F вычисляются величины S x , S y , S, которые показывают расположение тела по отношению к цели.

1. Исследуйте, что означает знак S x и S y в различные моменты времени. 

Вывод.

2. Исследуйте, как изменяется S при движении тела.

Вывод. Полное расстояние до цели сначала уменьшается, а потом увеличивается.

3. Подберите исходные данные (начальную скорость и угол бросания), соответствующие вариантам движения тела, представленным на рисунке 3.7, на свободном поле электронной таблицы (таблица 4).

ЭКСПЕРИМЕНТ 5. Подбор исходных значений для попадания в цель

Прежде всего заметим, что существует бесконечное множество вариантов исходных данных для попадания в цель. Наша задача - подобрать один вариант.

1. По столбцу F определите наименьшее значение S . В этот момент тело ближе всего пролетает к цели.

2. Постройте столбец G анализа попадания. Будем считать, что тело попало в цель, если расстояние до цели стало меньше заданной точности (ячейка $D$10) . Для этого в ячейку G16 введите формулу =ЕСЛИ(F16<$D$10; «попал»; «мимо») .

3. Изменяйте исходные данные, чтобы получить наилучшее приближение к цели.

4. Результаты исследования запишите на свободном поле электронной таблицы (таблица 5).

5. Подберите еще один набор исходных данных, при котором тело попадет в цель «навесом», то есть после прохода наивысшей точки подъема.

6. Измените координаты цели и подберите значения начальной скорости и угла бросания для нового положения цели.

Результаты и выводы, полученные в экспериментах, оформите в виде отчета в текстовом документе. В отчете приведите ответы на следующие вопросы:

1. Как движется тело, брошенное под углом к горизонту?
2. Как определить наивысшую точку подъема?
3. Как определить дальность полета?
4. Как изменяется наибольшая высота подъема при увеличении начальной скорости и неизменном угле броска?
5. Как изменяется дальность полета при увеличении начальной скорости и неизменном угле броска?
6. Как изменяется наибольшая высота подъема при увеличении угла бросания и неизменной начальной скорости?
7. Как изменяется дальность полета при увеличении угла бросания и неизменной начальной скорости?
8. Как по расчетам определить положение тела по отношению к цели в каждый момент времени? Как это определить по таблице расчетов?
9. Как изменяется расстояние от тела до цели при движении и как это определить по таблице расчетов?

ЗАДАЧА 3.25*. Движение парашютиста

* Задача повышеной сложности

I этап. Постановка задачи

ОПИСАНИЕ ЗАДАЧИ

Парашютист при падении к земле испытывает действие силы тяжести и силы сопротивления воздуха. Экспериментально установлено, что сила сопротивления зависит от скорости движения: чем больше скорость, тем больше сила. При движении в воздухе эта сила пропорциональна квадрату скорости с некоторым коэффициентом сопротивления k , который зависит от конструкции парашюта и веса человека R сопр = kV 2 .Каково должно быть значение этого коэффициента, чтобы парашютист приземлился на землю со скоростью не более 8 м/с , не представляющей опасности для здоровья?

Определите цели моделирования и проведите формализацию задачи.

II этап. Разработка модели

ИНФОРМАЦИОННАЯ МОДЕЛЬ

Составьте информационную модель самостоятельно.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

На рисунке 3.8 указаны силы, действующие на парашютиста. Согласно второму закону Ньютона движение под действием сил можно записать равенством. Проецируем это равенство на ось движения, подставим выражение для силы сопротивления воздуха mа = mg - kV 2 .

Получим формулу для вычисления ускорения

Будем рассчитывать скорость и расстояние, которое пролетел парашютист через равные промежутки времени △t . Формула для вычисления моментов времени имеет вид: t i+1 + t i + △t . 

где V i - скорость в начале промежутка (V o - начальная скорость). Скорость в конце промежутка (и, соответственно, в начале следующего) вычисляется по формуле равноускоренного движения

Расстояние, которое пролетел парашютист, равно сумме расстояния, пройденного к началу очередного промежутка времени (S i ), и расстояния, пройденного на этом промежутке:

КОМПЬЮТЕРНАЯ МОДЕЛЬ

Для моделирования выберем среду электронной таблицы. В этой среде информационная и математическая модели объединяются в таблицу, которая содержит три области:

♦ исходные данные;
♦ промежуточные расчеты;
♦ результаты.

1. Заполните область исходных данных.

2. Заполните расчетные столбцы А, В, С, D, в которых вычисляются параметры движения парашютиста:

Время;
скорость;
расстояние;
ускорение.

3. Введите формулы в расчетные ячейки. Пример заполнения расчетной таблицы: 

III этап. Компьютерный эксперимент

ПЛАН ЭКСПЕРИМЕНТА

ТЕСТИРОВАНИЕ

Провести тестовый расчет компьютерной модели по данным, приведенным в таблице.

ЭКСПЕРИМЕНТ 1

Исследовать движение тела под действием силы тяжести и сопротивления воздуха.

ЭКСПЕРИМЕНТ 2

Подобрать значение коэффициента сопротивления k для безопасного приземления парашютиста. 

ЭКСПЕРИМЕНТ 3

Исследовать зависимость скорости, ускорения от начальной скорости движения.

ЭКСПЕРИМЕНТ 4

Исследовать, как изменяется расстояние полета до стабилизации скорости падения.

ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ

ТЕСТИРОВАНИЕ

1. Сравните результаты тестового расчета с результатами, приведенными в примере расчета. Пример тестового расчета:

2. Постройте диаграмму изменения скорости, ускорения и расстояния в зависимости от времени.

ЭКСПЕРИМЕНТ 1. Исследование движения тела с учетом сопротивления воздуха

1. Определите по диаграмме и по таблице, как изменяется с течением времени скорость движения парашютиста. Через сколько секунд наступает стабилизация скорости падения?

2. Определите по диаграмме и по таблице, как изменяется с течением времени ускорение парашютиста.

3. Определите по диаграмме и по таблице, какое расстояние пролетит парашютист до стабилизации скорости движения. Результаты поместите на свободном поле в электронной таблице.

4. Измените шаг времени (0,1 с) и определите скорость стабилизации движения, расстояние полета до стабилизации. Результаты исследования приведите в таблице.

ЭКСПЕРИМЕНТ 2. Подбор коэффициента сопротивления

Изменяя значение коэффициента k (ячейка СЗ) , подберите скорость стабилизации движения, безопасную для приземления тренированного человека (8 м/с) .

ЭКСПЕРИМЕНТ 3. Исследование стабилизации скорости и расстояния в зависимости от начальной скорости

Парашютист, выпрыгнув из самолета, некоторое время летит в свободном падении, набирает достаточно большую скорость движения и только потом раскрывает парашют.

1. Измените значение начальной скорости (10 м/с) .

2. По таблице расчетов определите, как изменится:

Начальное ускорение;
скорость стабилизации;
расстояние полета до стабилизации скорости.

3. Результаты эксперимента запишите на свободном поле электронной таблицы. Сделайте вывод.

Результаты эксперимента 3:

Примечание. Обратите внимание, как изменяется начальное ускорение. Учтите, что оно не может быть большим, так как ускорение более 3g (30 м/с2) вызывает очень большие перегрузки.

IV этап. Анализ результатов моделирования

По результатам компьютерного эксперимента ответить на следующие вопросы:

1. Как изменяется скорость парашютиста с течением времени?
2. Как изменяется скорость парашютиста при изменении коэффициента сопротивления?
3. Каким должен быть коэффициент сопротивления, чтобы парашютист опустился на землю со скоростью 8 м/с?
4. Как изменяется скорость движения и как зависит установившаяся скорость равномерного движения парашютиста от начальной скорости?
5. Через сколько секунд после начала движения скорость парашютиста можно считать установившейся?
6. На какой высоте от земли парашютист должен раскрыть парашют, чтобы приземлиться с заданной скоростью.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

3.26. Баскетболист.

Пользуясь построенной моделью движения тела, брошенного под углом, рассчитать, с какой начальной скоростью и под каким углом нужно бросить баскетбольный мяч, чтобы попасть в кольцо.

При расчетах учесть следующие условия:

Начальная скорость мяча при броске может изменяться в пределах до 15 м/с;
координаты кольца у = 3 м, х = 0,5 ÷ 7 м;
точность попадания связана с диаметром кольца и равна △ = 20 см;
мяч должен попасть в кольцо «навесом», то есть после прохода наивысшей точки подъема.

Измените математическую и компьютерную модели движения тела, брошенного под углом, так, чтобы по ним можно было рассчитать движение тела, брошенного с некоторой начальной высоты y 0

3.27. Спасение утопающего.

С какой скоростью и под каким углом надо бросить с борта спасательного судна круг утопающему? При расчетах учесть следующие условия:

расстояние утопающего от корабля;
точность попадания равна △ = 0,5 м;
угол бросания может быть отрицательным;
высоту борта корабля над уровнем моря.

3.28. Акробаты.

Многие видели в цирке такой акробатический номер. Один акробат встает на прыжковую доску с одной стороны, второй прыгает на другой конец. С какой начальной скоростью и под каким углом должен взлететь вверх первый акробат, чтобы опуститься точно на плечи третьего участника номера? При расчетах учесть следующие условия:

Начальная скорость может изменяться в пределах до 10 м/с;
высоту и удаление третьего акробата;
точность попадания равна △ = 0,1 м.

К этому уроку прилагается 3D-сцена

Краткое предисловие

Собственно говоря, в предыдущих уроках уже были упомянуты отдельные аспекты физики в Cinema 4D: так, например, в самом первом уроке на данном сайте мы с вами роняли шар на плоскую поверхность , позже физическую модель Cinema 4D рассматривали как один из способов моделирования генератора бесконечного движения . Но до сих пор это были лишь частные, крайне поверхностные и самые примитивные аспекты физики.

В данном же уроке мы с вами перейдём к самому интересному: к углублённому изучению физики в Cinema 4D на основе конкретного примера - мы попробуем создать и настроить (хотя бы в самом примитивном варианте) вполне работоспособную физическую модель движения автомобиля по пересечённой местности, имитирующую в общих чертах те же принципы, по которым автомобиль движется в реальном мире.

Необходимость применения физической модели перемещения автомобиля кроется в словах «по пересечённой местности». В большинстве случаев при моделировании автомобильного движения нет никакой необходимости в использовании физической модели: автомобили равномерно движутся по траектории (именно такой транспортный поток мы с вами учились создавать из одной модели автомобиля , помните?), визуально практически никак не взаимодействуя с окружающей обстановкой, и это легко и просто изобразить простыми средствами, не прибегая к физике. Однако как только речь заходит о сложном рельефе местности, по которой едет автомобиль, или о неординарном поведении самого автомобиля (дрифт, заносы или столкновения) - вот тут-то и настаёт черёд физики, если только мы с вами не хотим вручную расставлять огромное количество ключей и править кривые поведения трёхмерной модели для каждой секунды поведения последней (и это без гарантии визуального праводоподобия финального рендера).

Цели и задачи

Для начала определимся с целями и задачами. В данном уроке наша с вами цель - изобразить более-менее правдоподобное поведение автомобиля при движении по неровной поверхности. Конкретнее: автомобиль должен подпрыгивать и крениться при наезде на неровности, а также вывешивать колёса над выбоинами. А ещё, разумеется, он должен замедляться при преодолении нервностей и ускоряться на ровных участках.

Если бы не ускорение и замедление автомобиля в зависимости от рельефа, то возможно, мы с вами упростили бы себе задачу, «подвесив» автомобиль к движущемуся по заданной траектории невидимому «лидеру» - в этом случае автомобиль уподобился бы детским санкам, скорость которых зависит не от высоты снежных сугробов под полозьями, а от скорости шага отца, который тащит на санках сына. В нашем же случае нам с вами такой вариант решения проблемы не подходит, то есть придётся оборудовать модель автомобиля самым что ни на есть работающим двигателем. Для максимальной эффектности сделаем наш автомобиль заднеприводным внедорожником.

Приступаем?

Начнём с моделирования внешнего вида автомобиля (именно внешнего вида, а не физической модели - это не одно и то же!). Состоять наш с вами автомобиль будет всего лишь из пяти трёхмерных элементов: кузов и четыре колеса. Надеюсь, вам понятно, что каждое колесо должно быть отдельным элементом модели. Кроме того, каждое из колёс желательно сделать цельным (монолитным), то есть состоящим из одного-единственного элемента, а не из набора элементов, иначе впоследствии вы столкнётесь с массой сложностей - вам придётся скреплять между собой все элементы каждого из колёс при помощи физических модификаторов, что, на мой взгляд, было бы совершенно излишней тратой времени. Основной принцип, исходя из которого мы с вами разделили элементы модели - это возможность последующего визуального смещения элементов друг относительно друга во время движения внедорожника.

Обратите внимание, что в днище кузова внедорожника предусмотрены вырезы для колёс - оговорюсь сразу, что их отсутствие не помешало бы работе нашей будущей физической модели (позже вы сами в этом убедитесь), но во время просмотра анимации было бы видно проходящие насквозь через днище колёса, что, конечно, было бы грубой визуальной ошибкой.

А теперь переходим к самому главному: к созданию непосредственно физической модели внедорожника. Возможно, вы сразу же предположите, что наступила пора прикрепить колёса к кузову. Ни в коем случае! Ни сейчас, ни позже. И вот почему. Дело в том, что прикрепи вы колёса непосредственно к кузову - у вас опять-таки возникла бы куча сложностей: физическая модель Cinema 4D воспринимала бы колёса как находящиеся внутри кузова (т. е. как бы завязшие внутри него), и во что бы то ни стало пыталась бы высвободить их, вследствие чего вместо более-менее правдоподобного поведения колёс вы увидели бы главным образом их мелкую, безостановочную вибрацию и минимум реакции на физическое взаимодействие с прочими окружающими внедорожник объектами. Конечно, проблема эта вполне решается тонкой и длительной настройкой значений динамики сцены и моделей, вроде интервалов, по достижении которых начинается взаимодействие трёхмерных элементов, но мы с вами пойдём более простым путём.

Мы с вами пойдём более простым путём - и создадим на сей раз не визуальную, а физическую модель кузова автомобиля. В исполнении автора - это самый обычный полигональный куб. В вашем это может быть любой другой полигональный объект - главное, чтобы он не был виден под кузовом внедорожника, и чтобы он был полигональной моделью, края которой находятся достаточно далеко от колёс. Этот элемент мы условно назовём весовым центром.

Почему именно так, спросите вы? Почему это не может быть NULL-объект или сплайн?

Потому что созданный нами весовой центр по определению и в силу своего наименования предназначен для активного участия в физической модели внедорожника. Ни сплайны, ни NULL-объекты, будучи наделены физическими характеристиками, не используют последние, так как не имеют физической поверхности.

Итак, весовой центр внедорожника создан. Переходим к прикреплению колёс. При отсутствии физической модели мы просто подчинили бы их кубу (или даже кузову) в менеджере объектов, и этого было бы вполне достаточно. В нашем же случае колёса должны быть прикреплены не жёстко, а с учётом определённой физической свободы, то есть возможности слегка смещаться относительно весового центра при возникновении физического взаимодействия с другими объектами в сцене (например, с неровностями дорожного покрытия).

Именно для такого вида крепления в Cinema 4D предусмотрены объекты типа «Connector» (от англ. «connect» - «соединять»). Переходим в верхнее меню, ищем пункт «Simulation», в выпадающем из этого пункта меню выбираем подпункт «Dynamics» и в выпадающем подменю жмём «Connector».

Мы видим, что в рабочем окне появился новый объект, а в менеджере объектов - его наименование. Начнём с правого переднего колеса. Размещаем коннектор в точке, где расположен геометрический центр колеса, которое будет прикреплено с помощью коннектора к кузову - при этом сам геометрический центр колеса должен быть расположен в том месте, где у колеса как бы находится центр колёсной ступицы.

Теперь нужно настроить коннектор. Выделяем его наименование в менеджере объектов и видим открывшееся ниже окно свойств.

Первый параметр, значение которого нам следует изменить - это тип соединения (параметр «Type»), от него зависит, по каким закономерностям будет смещаться колесо относительно кузова. Очевидно, наиболее подходящим типом соединения в нашем случае будет «Wheel Suspension». В поле напротив слов «Object A» перетаскиваем из менеджера объектов наименование весового центра, на изображении ниже он обозначен как «Base» - это объект, к которому мы с вами прикрепляем колесо. В поле напротив слов «Object B» перетаскиваем наименование колеса (на изображении обозначено как «Wheel_FR», от сокращения «Wheel Front Right») - это объект, который мы с вами прикрепляем. Параметры «Attachment A» и «Attachment B» трогать не будем - они обозначают, где у объектов находятся центры масс, и выставленные по умолчанию значения в данном случае нас вполне устраивают.

Переходим к тонкой настройке коннектора.

Параметр «Ignore Collisions» («игнорировать взаимодействие») предназначен для случая, когда вы хотите избежать физического взаимодействия колеса с весовым центром - например, если параметры коннектора позволяют колесу отклоняться на угол до 45 градусов, но колесо при этом упирается в объект, к которому прикреплено, и не может отклониться на максимально разрешённый угол, то эта настройка может помочь. Параметр «Steering Angle» («Угол поворота») - это и есть тот самый максимально разрешённый угол отклонения колеса от своего первоначального положения. Параметр «Suspension Rest Position» определяет смещение колеса по вертикали в состоянии покоя (то есть в те моменты, когда колесо ни с чем не взаимодействует). В нашем с вами случае значение составляет -15 см. - если изменить его до -25, то кузов внедорожника будет поднят по отношению к колёсам ещё выше, нежели в данный момент, и дорожный просвет увеличится, но при этом понизится устойчивость внедорожника, так как весовой центр окажется выше - не правда ли, это уже напоминает баланс устойчивости автомобилей в реальном мире? От значения параметра «Suspension Stiffness» зависит мягкость подвески. Чем меньше значение, тем мягче будет подвеска. Параметр «Suspension Dumping» определяет «прыгучесть» подвески. Ну и наконец, при желании можно активировать параметры «Lower Limit Y» и «Upper Limit Y» и указать для них значения дистанций, на расстояния больше которых колесо отклониться не сможет.

Закончив настройку коннектора, повторяем ту же операцию - начиная с создания нового коннектора - для второго переднего колеса, на сей раз левого. Вместо путешествий по верхнему меню, как вы, вероятно, уже сообразили, можно просто найти созданный нами ранее коннектор правого переднего колеса, и изо всех сил вдавив и не отпуская клавишу «Ctrl» на клавиатуре, перетащить наименование коннектора на свободное место в менеджере объектов - после выполнения этой операции мы с вами получим новую копию коннектора, да к тому же унаследовавшую от своего оригинала все настройки. Главное - не забудьте сменить в поле «Object B» свойств нового коннектора наименование правого колеса на наименование левого.

С передними колёсам закончили. Переходим к задним.

И сразу же сталкиваемся с несколько неочевидным на первый взгляд вопросом: сколько двигателей должно быть у нашего внедорожника? Что за странный вопрос, скажете вы - один, естественно.

Объясню, с чем связан такой вопрос. В реальном механизме автомобиля крутящий момент передаётся на оба ведущих колеса одновременно через достаточно сложную систему механических приводов. Нам с вами нет смысла моделировать эту систему приводов, так как у нас нет задачи визуализировать внутреннее устройство внедорожника, а значит, вместо полноценной работы двигателя мы можем позволить себе любую его упрощённую физическую имитацию, лишь бы ведущие колёса крутились и толкали автомашину вперёд.

Таким образом, у нас с вами имеется два альтернативных решения: если нам позарез требутся изобразить раздельную тягу двух ведущих колёс , мы можем добавить в виртуальную конструкцию два отдельных двигателя, каждый из которых будет крутить «своё» колесо. Если же моделирование раздельной тяги нам с вами не нужно, то наиболее эффективным и простым способом привести автомобиль в движение будет создание так называемой «колёсной пары» - два наглухо сцементированных вместе колеса, которые приводятся в движение одним мотором.

В данном уроке мы с вами выберем второй, более простой способ - создание колёсной пары и её вращение одним мотором. С оговоркой, что в принципе при желании можно усложнить и этот способ - к примеру, вращать не колёсную пару, а ось с прикреплёнными к ней при помощи коннекторов ведущими колёсами, чтобы последние свободно вихлялись туда-сюда, как это уже настроено нами ранее для передних колёс. Впрочем, в данном уроке лишне усложнять себе задачу мы с вами не будем, есть желание - экспериментируйте самостоятельно на основе сцены, приложенной к этому уроку, ссылку на неё можно найти в начале урока.

Итак, решено - создаём колёсную пару: выделяем два задних колеса - можно в рабочем окне, можно в менеджер объектов, где вам удобнее - затем уже именно в менеджере объектов щёлкаем на любом из них правой клавишей мыши и в выпадающем контекстном меню ищем пункт «Connect+Delete» («Соединить и удалить»). Строкой выше в том же контекстном меню есть пункт «Connect» - он при объединении элементов создаёт новый объект, оставляя нетронутыми оригиналы объединяемых моделей, нам же с вами оригиналы раздельных задних колёс не понадобятся.

Мы видим, что задние колёса внедорожника стали одним трёхмерным элементом - то, что нам и требовалось.

Создаём ещё один коннектор - на сей раз для задней колёсной пары, и учитывая её монолитность, всего один, после чего настраиваем его. Располагаем его, естественно, в центре колёсной пары.

Теперь создаём мотор: верхнее меню, снова пункт «Simulation», выпадающее меню, подпункт «Dynamics», в выпадающем меню подпункт «Motor».

Располагаем созданный мотор там же, где коннектор для колёсной пары - посерединке между задними колёсами (или, выражаясь научно, в геометрическом центре задней колёсной пары), затем выделяем его наименование в менеджере объектов, плавно премещаем взгляд в открывшееся ниже окно свойств мотора и приступаем к настройке.

В поле рядом со словами «Object A» перетаскиваем из менеджера объектов наименование задней колёсной пары (на изображении оно обозначено как «Back Wheels»). В поле рядом со словами «Object B» ничего не перетаскиваем. Для параметра «Type» («Тип») выбираем значение «Angular» («угловой») - всё правильно, ведь для движения внедорожника созданный нами мотор должен непрерывно поворачивать ведущую колёсную пару на определённый угол. В качестве значения для параметра «Mode» («Режим») указываем «Regulate Speed» («Постоянная скорость»). Ну и наконец указываем числовые значения для параметров «Angular Target Speed» («скорость вращения цели») и «Torque» («крутящий момент»).

Вероятно, вы уже готовы запустить анимацию и проверить полученный результат. Если так, то - несколько рановато: ведь мы с вами выполнили только одну часть работы - настроили физическое воздействие на объекты, тогда как самих физических объектов у нас с вами пока нет. А колёса, скажете вы, а кузов, а весовой куб? Верно, полигональные модели созданы, но физически для сил воздействия ни колёс, ни кузова, ни весового куба пока не существует - пока колёсам, кузову и весовому кубу не назначен тег динамики. Ибо именно назначенный полигональному элементу трёхмерной сцены тег динамики обозначает, что данный элемент участвует во взаимодействии с другими элементами, обладающими динамическими характеристиками.

Приступаем к настройке физических характеристик внедорожника. А заодно и выстраиваем иерархическую структуру элементов, из которых он состоит. Первым делом создаём группу, в которой будут собраны все элементы автомобиля (если этого ещё не сделано) - это можно сделать, объединив несколько первых попавшихся под руку элементов при помощи комбинации клавиш Alt+G (напоминаю, что в отличие от общепринятого в Cinema 4D способа последовательного раздельного нажатия клавиш, эта комбинация нажимается одновременно!), либо создав NULL-объект.

Далее обзываем созданную группу неким уникальным, неповторимым и незабываемым словом (к примеру, автор назвал её «CAR») и запихиваем в неё все относящиеся к внедорожнику элементы: кузов, колёса, коннекторы, весовой куб и мотор.

Теперь обозначаем элементы группы как участников физического взаимодействия с окружающей физической моделью: выделяем наименование группы, щёлкаем на нём правой клавишей мыши, в выпадающем меню наводим курсор мыши на пункт «Dynamics Tags» («Теги динамики») и в выпадающем из последнего подменю выбираем единственный пункт - «Dynamics Body».

Если до сих пор вы внимательно знакомились с данным уроком, то, возможно, спросите: как группа «CAR», будучи NULL-объектом, может физически взимодействовать в физической модели? Верно, сам NULL-объект - никак. Зато свойства динамики могут унаследовать от него все подчинённые ему элементы, при этом отпадает необходимость назначать тег динамики каждому элементу индивидуально. Главное - правильно настроить тег динамики группы. Настраиваем: выделяем тег и в открывшемся ниже окне свойств выбираем вкладку «Dynamics», в которой активируем параметр «Enabled» (тем самым включая физику взаимодействия) и выбираем значение «On» для параметра «Dynamic» (тем самым указывая участие группы во всех общих для сцены физических правилах, типа гравитации и пр.)...

После чего переходим во вкладку «Collision» («Соприкосновение») в том же окне свойств и указываем значения, заставляющие элементы группы наследовать правила динамики: «Apply Tag to Children» («распространять действие тега на дочерние элементы») для параметра «Inherit Tag» («Наследование»), «All» («всё») для «Individual Elements» («Отдельные элементы»), галочку напротив «Self Collisions» («Собственное взаимодействие») и «Automatic (MoDynamics)» для «Shape» («Контур»). Остальные параметры настраиваем на свой вкус.

Тут будет уместно наконец-то вспомнить про кузов внедорожника. По нашей задумке, он также должен взаимодействовать с окружающей физической моделью трёхмерной сцены - например, разбрасывать носовой частью стену из картонных ящиков, - но при этом не должен взаимодействовать с другими элементами своей же группы - с весовым кубом и колёсами. Чтобы добиться такого результата, мы с вами подчиним его весовому кубу и назначим кузову индивидуальный тег динамики - точно так же, как группе элементов автомобиля, - но в теге динамики кузова отключим параметр «Dynamic» (укажем для него значение «Off») во вкладке «Dynamics» (обратите внимание, параметр «Enabled» остаётся активированным, иначе кузов вообще перестанет участвовать в физической модели сцены, и любое оказавшееся на пути внедорожника препятствие свободно пройдёт насквозь через кузов!). Во вкладке «Collision» назначенного кузову тега динамики для параметров «Inherit Tag» и «Individual Elements» можно указать соответственно «None» и «Off» - у кузова нет подчинённых элементов, которым следовало бы передавать динамические свойства кузова.

Всё, что осталось - это добавить в трёхмерную сцену неоднократно упоминавшуюся выше окружающую физическую модель - некий неровный рельеф, который в финальной анимации выявлял бы физически правдоподобную реакцию автомобиля на взаимодействие с ухабами. В приложенной к уроку сцене - это грубое подобие некоей арены с усеянной буграми сердцевиной.

В заключение

В данном уроке мы с вами изучили создание простейшей физической модели движения автомобиля - без каких-либо дополнительных плагинов и модулей, штатными средствами Cinema 4D. В уроке, как вы заметили, не рассматривается моделирование поворотов, созданная нами модель способна к движению только по прямой - разумеется, если только неровности рельефа под колёсами не изменят траекторию движения (что и происходит в нижеприведённом видеоролике). К слову говоря, автор намеренно настроил параметры физической модели трёхмерной сцены так, чтобы движение внедорожника было как бы гиперболизировано, с целью наглядно продемонстрировать взаимодействие колёс и кузова машины с неровностями. Кроме того, в приложенную к уроку сцену входят и другие, не упомянутые в уроке элементы, предназначенные для съёмки и освещения. Впоследствии, возможно, на сайте будут рассмотрены и более сложные физические модели.

Финальный результат в виде анимации.

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

РЕСПУБЛИКАНСКИЙ ИНСТИТУТ ИННОВАЦИОННЫХ ТЕХНОЛОГИЙ

КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Курсовая работа

Дисциплина «Математическое моделирование»

Тема: «Моделирование движения парашютиста»

Введение

1. Свободное падение тела с учетом сопротивления среды

2. Формулировка математической модели и ее описание.

3. Описание программы исследования с помощью пакета Simulink

4. Решение задачи программным путем

Список использованных источников

Введение

Формулировка проблемы :

Катапульта выбрасывает манекен человека с высоты 5000 метров. Парашют не раскрывается, манекен падает на землю. Оценить скорость падения в момент удара о землю. Оценить время достижения манекеном предельной скорости. Оценить высоту, на которой скорость достигла предельного значения. Построить соответствующие графики, провести анализ и сделать выводы.

Цель работы :

Научиться составлять математическую модель, решать дифференциальные уравнения программными средствами (используется язык технических вычислений MatLAB 7.0, пакет расширения Simulink) и анализировать полученные данные о математической модели.

1. Свободное падение тела с учетом сопротивления среды

При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту, относительно несложную, задачу нельзя решить средствами “школьной” физики: таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.

Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение, где определяется свойствами среды и формой тела. Например, для шарика - это формула Стокса, где - динамическая вязкость среды, r - радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм = 0,0182 H.c.м-2 для воды 1,002 H.c.м-2 , для глицерина 1480 H.c.м-2.

Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (в движение станет равномерным).

(1)

Пусть r= 0,1 м, = 0,8 кг/м (дерево). При падении в воздухе м/с, в воде 17 м/с, в глицерине 0,012 м/с.

На самом деле первые два результата совершенно не соответствуют действительности. Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится пропорциональной квадрату скорости: . Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если , то вкладом можно пренебречь (это конкретный пример ранжирования факторов). О величине k2 известно следующее: она пропорциональна площади сечения тела S, поперечного по отношению к потоку, и плотности среды и зависит от формы тела. Обычно представляют k2 = 0,5сS, где с - коэффициент лобового сопротивления - безразмерен. Некоторые значения с (для не очень больших скоростей) приведены на рис.1.

При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз уменьшается. Для шара оно становится приблизительно равным 0,1. Подробности можно найти в специальной литературе.

Вернемся к указанной выше оценке, исходя из квадратичной зависимости силы сопротивления от скорости.

для шарика

(3)

Рис 1 . Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму

Примем r = 0,1 м, =0,8.103 кг/м3 (дерево). Тогда для движения в воздухе (= 1,29 кг/м3) получаем 18 м/с, в воде(= 1.103 кг/м3) 0,65 м/с, в глицерине (= 1,26.103 кг/м3) 0,58 м/с.

Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим, что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина справедливо обратное утверждение. Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения - уравнение второго закона Ньютона с учетом двух сил, действующих на тело: силы тяжести и силы сопротивления среды:

(4)

Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем

(5)

Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения скорости со временем, если все параметры, входящие в уравнение (7) заданы? При такой постановке модель носит сугубо дескриптивный характер. Из соображений здравого смысла ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента, , и соответствующую установившуюся скорость можно найти из условия =0, решая не дифференциальное, а квадратное уравнение. Имеем

(6)

(второй - отрицательный - корень, естественно, отбрасываем). Итак, характер движения качественно таков: скорость при падении возрастает от до . Как и по какому закону – это можно узнать, лишь решив дифференциальное уравнение (7).

Однако даже в столь простой задаче мы пришли к дифференциальному уравнению, которое не относится ни к одному из стандартных типов, выделяемых в учебниках по дифференциальным уравнениям, допускающих очевидным образом аналитическое решение. И хотя это не доказывает невозможность его аналитического решения путем хитроумных подстановок, но они не очевидны. Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию нескольких алгебраических и трансцендентных функций – а как найти закон изменения во времени перемещения? Формальный ответ прост:

(7)

но шансы на реализацию этой квадратуры уже совсем невелики. Дело в том, что класс привычных нам элементарных функций очень узок, и совершенно обычна ситуация, когда интеграл от суперпозиции элементарных функций не может быть выражен через элементарные функции в принципе. Математики давно расширили множество функций, с которыми можно работать почти так же просто, как с элементарными (т. е. находить значения, различные асимптотики, строить графики, дифференцировать, интегрировать). Тем, кто знаком с функциями Бесселя, Лежандра, интегральными функциями и еще двумя десятками других, так называемых специальных функций, легче находить аналитические решения задач моделирования, опирающихся на аппарат дифференциальных уравнений. Однако даже получение результата в виде формулы не снимает проблемы представления его в виде, максимально доступном для понимания, чувственного восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни, синусы и тем более специальные функции, детально представить себе описываемый ею процесс - а именно это есть цель моделирования.

В достижении этой цели компьютер - незаменимый помощник. Независимо от того, какой будет процедура получения решения - аналитической или численной, - задумаемся об удобных способах представления результатов. Разумеется, колонки чисел, которых проще всего добиться от компьютера (что при табулировании формулы, найденной аналитически, что в результате численного решения дифференциального уравнения), необходимы; следует лишь решить, в какой форме и размерах они удобны для восприятия. Слишком много чисел в колонке быть не должно, их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря, гораздо больше шага, с которым решается дифференциальное уравнение в случае численного интегрирования, т.е. далеко не все значения и , найденные компьютером, следует записывать в результирующую таблицу (табл. 2).

Таблица 2

Зависимость перемещения и скорости падения от времени (от 0 до 15 с)

t(c)	S(m)	(м/с)	t(c)	S(m)	(м/с)

Кроме таблицы необходимы графики зависимостей и ; по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественное понимание процесса.

Еще один элемент наглядности может внести изображение падающего тела через равные промежутки времени. Ясно, что при стабилизации скорости расстояния между изображениями станут равными. Можно прибегнуть и к цветовой раскраске - приему научной графики, описанному выше.

Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый фиксированный отрезок пути, пройденный телом - скажем, через каждый метр или каждые 100 метров - смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки не сравняются. Таким образом, восприятию помогают элементы мультимедиа. Поле для фантазии здесь велико.

Приведем конкретный пример решения задачи о свободно падающем теле. Герой знаменитого фильма “Небесный тихоход” майор Булочкин, упав с высоты 6000 м в реку без парашюта, не только остался жив, но даже смог снова летать. Попробуем понять, возможно, ли такое на самом деле или же подобное случается только в кино. Учитывая сказанное выше о математическом характере задачи, выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений.

(8)

Разумеется, это не только абстрактное выражение обсуждаемой физической ситуации, но и сильно идеализированное, т.е. ранжирование факторов перед построением математической модели произведено. Обсудим, нельзя ли произвести дополнительное ранжирование уже в рамках самой математической модели с учетом конкретно решаемой задачи, а именно - будет ли влиять на полет парашютиста линейная часть силы сопротивления и стоит ли ее учитывать при моделировании.

Так как постановка задачи должна быть конкретной, мы примем соглашение, каким образом падает человек. Он опытный летчик и наверняка совершал раньше прыжки с парашютом, поэтому, стремясь уменьшить скорость, он падает не “солдатиком”, а лицом вниз, “лежа”, раскинув руки в стороны. Рост человека возьмем средний - 1,7 м, а полуобхват грудной клетки выберем в качестве характерного расстояния - это приблизительно 0,4 м. для оценки порядка величины линейной составляющей силы сопротивления воспользуемся формулой Стокса. Для оценки квадратичной составляющей силы сопротивления мы должны определиться со значениями коэффициента лобового сопротивления и площадью тела. Выберем в качестве коэффициента число с=1,2 как среднее между коэффициентами для диска и для полусферы (выбор дня качественной оценки правдоподобен). Оценим площадь: S = 1,7 ∙ 0,4 = 0,7(м2).

В физических задачах на движение фундаментальную роль играет второй закон Ньютона. Он гласит, что ускорение, с которым движется тело, прямо пропорционально действующей на него силе (если их несколько, то равнодействующей, т.е. векторной сумме сил) и обратно пропорционально его массе:

Так для свободно падающего тела под действием только собственной массы закон Ньютона примет вид:

Или в дифференциальном виде:

Взяв интеграл от этого выражения, получим зависимость скорости от времени:

Если в начальный момент V0 = 0, тогда .

.

Выясним, при какой скорости сравняются линейная и квадратичная составляющие силы сопротивления. Обозначим эту скорость Тогда

Ясно, что практически с самого начала скорость падения майора Булочкина гораздо больше, и поэтому линейной составляющей силы сопротивления можно пренебречь, оставив лишь квадратичную составляющую.

После оценки всех параметров можно приступить к численному решению задачи. При этом следует воспользоваться любым из известных методов интегрирования систем обыкновенных дифференциальных уравнений: методом Эйлера, одним из методов группы Рунге - Кутта или одним из многочисленных неявных методов. Разумеется, у них разная устойчивость, эффективность и т.д. - эти сугубо математические проблемы здесь не обсуждаются.

Вычисления производятся до тех пор, пока не опустится на воду. Примерно через 15 с после начала полета скорость становится постоянной и остается такой до приземления. Отметим, что в рассматриваемой ситуации сопротивление воздуха радикально меняет характер движения. При отказе от его учета график скорости, изображенный на рисунке 2, заменился бы касательной к нему в начале координат.

Рис. 2. График зависимости скорости падения от времени

2. Формулировка математической модели и ее описание

парашютист падение сопротивление математическая модель

При построении математической модели необходимо соблюдение следующих условий:

Манекен массой 50 кг соответственно падают в воздухе с плотностью 1,225 кг/м3;

На движение влияют только силы линейного и квадратичного сопротивления;

Площадь сечения тела S=0.4 м2;

Тогда для свободно падающего тела под действием сил сопротивления закон Ньютона примет вид:

,

где a – ускорение тела, м/с2,

m – его масса, кг,

g – ускорение свободного падения на земле, g = 9,8 м/с2,

v – скорость тела, м/c,

k1 – линейный коэффициент пропорциональности, примем k1 = β = 6πμl (μ – динамическая вязкость среды, для воздуха μ = 0,0182 Н.с.м-2; l – эффективная длина, примем для среднестатистического человека при росте 1,7 м и соответствующем обхвате грудной клетки l = 0,4 м),

k2 – квадратичный коэффициент пропорциональности. K2 = α = С2ρS. В данном случае достоверно можно узнать лишь плотность воздуха, а площадь манекена S и коэффициент лобового сопротивления С2 для него определить сложно, можно воспользоваться полученными экспериментальными данными и принять K2 = α = 0,2.

Тогда получим закон Ньютона в дифференциальном виде:

Тогда можно составить систему дифференциальных уравнений:

Математическая модель при падении тела в гравитационном поле с учетом сопротивления воздуха выражается системой из двух дифференциальных уравнений первого порядка.

3. Описание программы исследования с помощью пакета Simulink

Для имитационного моделирования движения парашютиста в системе MATLAB используем элементы пакета расширения Simulink. Для задания величин начальной высоты - H_n, конечной высоты - H_ k, числа - pi, μ – динамическая вязкость среды - my, обхват - R, массе манекена m, коэффициент лобового сопротивления - c, плотность воздуха - ro, площадь сечения тела - S, ускорение свободного падения - g, начальная скорость - V_n используем элемент Constantнаходящийся в Simulink/Sources(рисунок 3).

Рисунок 3. Элемент Constant

Для операции умножения используем блок Product, находящийся в Simulink/MathOperations/Product (рисунок 4).

Рисунок. 4

Для ввода k1 – линейного коэффициента пропорциональности и k2 – квадратичного коэффициента пропорциональности используем элемент Gain, находящийся в Simulink/MathOperations/Gain(Рисунок. 5.)

Рисунок. 5

Для интегрирования – элемент Integrator. Находящийсяв Simulink/Continuous/Integrator. Рисунок. 6.

Рисунок. 6

Для вывода информации используем элементы Display и Scope. Находящиеся в Simulink/Sinks. (Рисунок. 7)

Рисунок. 7

Математическая модель для исследования с использованием вышеперечисленных элементов, описывающая последовательный колебательный контур приведена на рисунке 8.

Рисунок. 8

Программа исследований

1. Исследование графика зависимости высоты от времени и скорости от времени масса парашютиста равна 50кг.

Рисунок 9

Из графиков видно, что при расчете падения парашютиста массой 50 кг, следующие данные: максимальная скорость равна 41,6 м/с и время равно 18с, и должна достигаться через 800 м падения, т.е. в нашем случае на высоте около 4200 м.

Рисунок. 10

2. Исследование графика зависимости высоты от времени и скорости от времени масса парашютиста равна 100кг.

Рисунок 11

Рисунок 12

С массой парашютиста 100 кг.: максимальная скорость равна 58 м/с и время равно 15с, и должна достигаться через 500 м падения, т.е. в нашем случае на высоте около 4500 м. (рисунок. 11., рисунок. 12).

Выводы по полученным данным, которые справедливы для манекенов, отличающихся только массой, но с одинаковыми размерами, формой, типом поверхности и другими параметрами, определяющими внешний вид объекта.

Легкий манекен при свободном падении в гравитационном поле с учетом сопротивления среды достигает меньшей предельной скорости, но за меньший промежуток времени и, естественно, при одинаковой начальной высоте – в более низкой точке траектории, чем тяжелый манекен.

Чем тяжелее манекен, тем быстрее он достигнет земли.

4. Решение задачи программным путем

%Функция моделирования движения парашютиста

function dhdt=parashut(t,h)

global k1 k2 g m

% система ДУ первого порядка

dhdt(1,1)= -h(2);

% Моделирование движения парашютиста

% Васильцов С. В.

global h0 g m k1 k2 a

% k1-линейный коэффициент пропорциональности, определяющийся свойствами среды и формой тела. Формула Стокса.

k1=6*0.0182*0.4;

%k2-квадратичный коэффициент пропорциональности, пропорционален площади сечения тела, поперечного по

%отношения к потоку, плотности среды и зависит от формы тела.

k2=0.5*1.2*0.4*1.225

g=9.81; % ускорение свободного падения

m=50; % масса манекена

h0=5000; % высота

Ode45(@parashut,,)

r=find(h(:,1)>=0);

a=g-(k1*-h(:,2)+k2*h(:,2).*h(:,2))/m % вычисляемускорение

% Построение графика зависимости высоты от времени

subplot(3,1,1), plot(t,h(:,1),"LineWidth",1,"Color","r"),grid on;

xlabel("t, c"); ylabel("h(t), m");

title("Графикзависимостивысотыотвремени", "FontName", "Arial","Color","r","FontWeight","bold");

legend("m=50 kg")

% Построение графика зависимости скорости от времени

subplot(3,1,2), plot(t,h(:,2),"LineWidth",1,"Color","b"),grid on;

ylabel("V(t), m/c");

Title("Графикзависимостискоростиотвремени", "FontName", "Arial","Color","b","FontWeight","bold");

legend("m=50 kg")

% Построение графика зависимости ускорения от времени

subplot(3,1,3), plot(t,a,"-","LineWidth",1,"Color","g"),grid on;

text (145, 0,"t, c");

ylabel("a(t), m/c^2");

Title("Графикзависимостиускоренияотвремени", "FontName", "Arial","Color","g","FontWeight","bold");

legend("m=50 kg")

Экранная форма вывода графиков.

1. Вся физика. Е.Н. Изергина. – М.: ООО «Издательство «Олимп», 2001. – 496 с.

2. Касаткин И. Л. Репетитор по физике. Механика. Молекулярная физика. Термодинамика/ Под ред. Т. В. Шкиль. – Ростов Н/Д: изд-во «Феникс», 2000. – 896 с.

3. Компакт-диск «Самоучитель MathLAB». ООО «Мультисофт», Россия, 2005.

4. Методические указания к Курсовой работе: дисциплина Математическое моделирование. Движение тела при учете сопротивления среды. – Минск. РИИТ БНТУ. Кафедра ИТ, 2007. – 4 с.

5. Решение систем дифференциальных уравнений в Matlab. Дубанов А.А. [Электронный ресурс]. – Режим доступа: http://rrc.dgu.ru/res/exponenta/ educat/systemat/dubanov/index.asp.htm;

6. Энциклопедия д.д. Физика. Т. 16. Ч.1. с. 394 – 396. Сопротивление движению и силы трения. А. Гордеев. /Глав. ред. В.А. Володин. – М. Аванта+, 2000. – 448 с.

7. MatlabFunctionReference [Электронный ресурс]. – Режим доступа: http://matlab.nsu.ru/Library/Books/Math/MATLAB/help/techdoc/ref/.

Моделирование движения заключается в искусственном воспроизведении процесса движения физическими или математическими методами, например, с помощью ЭВМ.

В качестве примеров физических методов моделирования могут быть названы исследования движения на различных макетах элементов дороги или полигонные испытания, где создаются искусственные условия, имитирующие реальное движение транспортных средств. Простейшим примером физического моделирования может служить распространенный метод проверки возможностей маневрирования и постановки на стоянку различных транспортных средств с помощью их моделей на заданной площади, изображенной в уменьшенном масштабе.

Наибольшее значение имеет математическое моделирование (вычислительный эксперимент), основывающееся на математическом описании транспортных потоков. Благодаря быстродействию ЭВМ, на которых осуществляется такое моделирование, удается в минимальное время провести исследование влияния многочисленных факторов на изменения различных параметров и их сочетания и получить данные для оптимизации управления движением (например, для регулирования на пересечении), которые невозможно обеспечить натурными исследованиями.

В основу вычислительного эксперимента с применением ЭВМ легло понятие модели объекта, то есть математическое описание, соответствующее данной конкретной системе и отражающее с требуемой точностью поведение ее в реальных условиях. Вычислительный эксперимент дешевле, проще натурного, легко управляем. Он открывает путь к решению больших комплексных проблем и оптимальному расчету транспортных систем, научно обоснованному планированию исследований. Недостаток вычислительного эксперимента состоит в том, что применимость его результатов ограничена рамками принятой математической модели, построенной на основе закономерностей, выявленных с помощью натурного эксперимента.

Изучение результатов натурного эксперимента позволяет получить функциональные соотношения и теоретические распределения, исходя из которых строится математическая модель. Математическое моделирование в вычислительном эксперименте целесообразно разделить на аналитическое и имитационное. Процессы функционирования систем при аналитическом моделировании описываются с помощью некоторых функциональных отношений или логических условий. Учитывая сложность процесса дорожного движения, для упрощения приходится прибегать к серьезным ограничениям. Однако, несмотря на это, аналитическая модель позволяет находить приближенное решение задачи. При невозможности получения решения аналитическим путем модель может исследоваться с применением численных методов, позволяющих находить результаты при конкретных начальных данных. В этом случае целесообразно использовать имитационное моделирование, подразумевающее применение ЭВМ и алгоритмическое описание процесса вместо аналитического.

Широкое применение имитационное моделирование может найти для оценки качества организации движения, а также при решении различных задач, связанных с проектированием автоматизированных систем управления дорожным движением, например, при решении вопроса об оптимальной структуре системы. К числу недостатков имитационного моделирования относят частный характер получаемых решений, а также большие затраты машинного времени для получения статически достоверного решения.

Следует отметить, что в настоящее время область моделирования транспортных потоков находится в стадии формирования. Различные аспекты моделирования исследуются в МАДИ, ВНИИБД, НИИАТ и других организациях.